Click on a puzzle for its solution.
Start with a half cup of tea and a half cup of coffee. Take one tablespoon of the tea and mix it in with the coffee. Take one tablespoon of this mixture and mix it back in with the tea. Which of the two cups contains more of its original contents?
Insert any number of the symbols "+", "-", "×", "÷", "(", and ")" around and between the digits 8 3 8 3 to make an expression that evaluates to 24.
Extend the sequences:
A domino is exactly the same size as two squares of a standard 8x8 chessboard. 32 dominoes can be arranged to tile the chessboard with no gaps or overlaps. If two diagonally opposite corner squares are removed, is it possible to tile the remaining 62 squares with 31 dominoes?
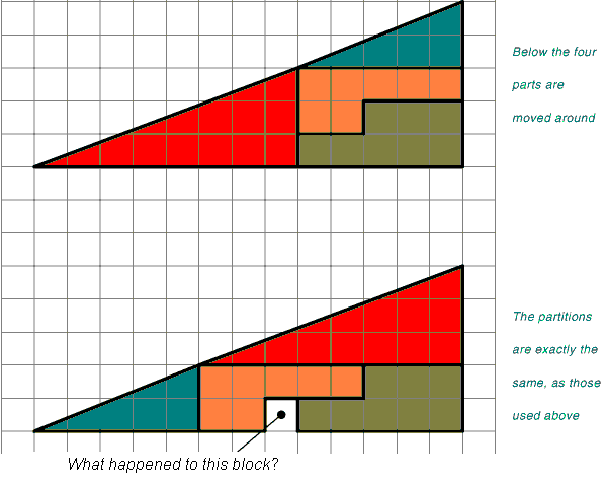
What is the minimum number of straight cuts that are required to cut a 3×3×3 cube of cheese into its 27 constituent 1×1×1 subcubes? The pieces may be moved around between cuts.
A worm eats its way into a 3×3×3 cube of cheese, visiting each of its 27 constituent 1×1×1 subcubes exactly once and moving between subcubes that share a face. Is it possible for the worm to end its meal at the center 1×1×1 subcube?
Two robots simultaneously land at different spots on a linear planet and drop their parachutes at their landing spots. They have no idea where the other robot landed, but their mission requires that they meet up. At every time step they can detect whether their current spot contains the other robot or a parachute, and they can move left or right to the next spot. Write a program for the robots to execute that guarantees that they will meet up.
You have made a deal with the devil to be immortal, except that every year on your birthday you must win a shell game to continue living. Every year it's the same old schtick: the devil appears at midnight in a sulphurous cloud and places 3 skulls on the table. One of the skulls has a gold tooth, but other than that they look identical. The devil hides a bead under one of the skulls, and then makes a series of moves with the skulls. Each move consists of the devil holding one skull in each hand and exchanging their locations. For some period of time during the skull moves the room is plunged into darkness, but it is still possible to count the number of moves that are being made. To win the game you must correctly guess which skull contains the bead in the final position. How can you keep winning forever?
You have 13 coins, one of which is a fake that has a different weight than a genuine coin. You are given a scales which can be used to weigh one set of coins against another set: it will either tip towards the heavier side or balance if both sides are equal. Find the fake coin using no more than 3 weighings.
You and a friend are in prison, but the warden offers to release you if you can pass a test that he explains to you as follows. First your friend will be brought into a room in which the warden has set up a chessboard with coins on some of the squares. The warden points to a particular square on the board, which may or may not contain a coin. After this your friend must select a square: if this square is empty then a coin will be put on it, and if it contains a coin then the coin will be removed. Your friend will then be removed from the room, and you will be brought in to examine the chessboard. You must point to a square on the chessboard, and if it is the same square that the warden pointed to then you pass the test. After giving this explanation the warden leaves to set up the chessboard, leaving you and your friend to talk. What strategy should you agree on to pass the test and gain your freedom?
A card magician leaves the room, and an audience member picks five cards at random from a standard 52 card deck and hands them to the magician's assistant. The assistant gives one card back to the audience member to hide, and deals the remaining four cards face up side by side onto the table. The magician re-enters the room, looks at the four cards on the table, and announces (to great applause) the hidden card that the audience member holds. How is the magic trick performed?
You are in prison with 1000 black balls, 1000 white balls and two large baskets. You must put all the balls in the baskets before next morning, when you will be brought grovelling before the king and the baskets placed next to him. He will first choose a basket at random, and then put in his hand and choose a ball at random. If it's white then you walk free, and if it's black then... gulp. How should you distribute the balls between the two baskets? (Oh, and if the king chooses an empty basket: it's the chop.)
Given the set X = {8462, 75693, 51089, 19293, 5664, 9826, 20781, 22195, 119392, 10352, 19987, 26532, 1662, 1894, 19556, 8325, 99810, 20029, 11828, 87206}, you must show that there exist at least two disjoint subsets of X having the same sum of elements. The solution does not involve exhibiting the sets. (Note that "disjoint" means that the two sets do not have any elements in common.)
Mr. S. and Mr. P. are both perfect logicians, being able to correctly deduce any truth from any set of axioms. Someone thinks of two numbers between 2 and 500 inclusive. He then adds them up and whispers the sum to Mr. Sum. He also multiplies them together and whispers the product to Mr. Product. The following conversation then ensues.
What were the original two numbers?
There is a road which forks. One path leads to heaven and the other to hell. At the junction there are two oracles who will answer any yes/no questions they are asked. One of them always tells the truth, and the other always lies. You do not know which is which. To discover which path leads to heaven, you are allowed to ask one yes/no question to one oracle.
At another fork there are three oracles, one of them always tells the truth, another of them always lies and the third tells the truth or lies purely at random. To discover the path to heaven you can now ask two yes/no questions (not necessarily to the same oracle).
You're on a gameshow, and there are three doors, only one of which contains a prize. As happens every week, you initially choose one door, then the gameshow host opens a different door to show that the prize was not behind that one. Finally you have the option of keeping your door or changing to the other closed door. Should you change?
See also the collections of mathematical puzzles compiled by Rustan Leino and Andrej & Elena.
A selection of mathematical puzzles chosen by Joe Leslie-Hurd.